计算机网络(五) 数据链路层
封装数据帧
数据链路层会为数据定界,即在数据的首部和尾部添加标识符,构成数据帧。
透明传输
数据链路层的透明传输指的是:无论传输的数据有什么样的比特组合,都应当能在链路上进行传输。控制符号仿佛“看不见”了,因此得名透明传输。
为了实现透明传输,对于有效数据中与控制符号完全相同的比特组合,必须采用适当的措施对其进行处理使其与控制符号区分开,并且要保证最终能正确地恢复为有效数据。
字符填充法:类似于转义字符的概念,在与控制符号相同的比特组合前加入一段特定的序列,使得后续的定长部分不会被视为控制字符。如果碰到与转义字符相同的原始信息,也同样在其前面添加一段转义字符。恢复时,将每个转义字符去掉即可。图示如下:
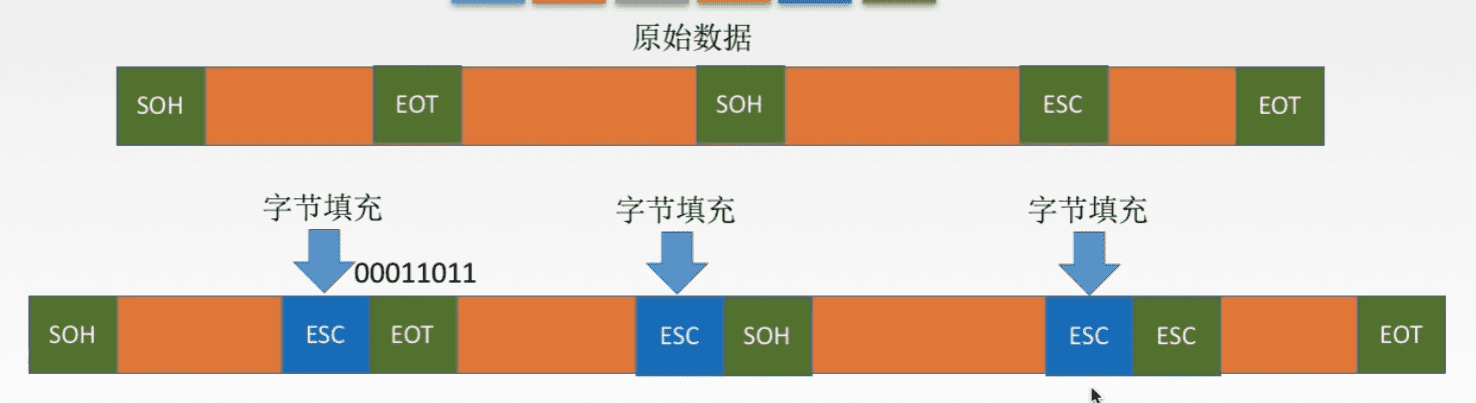
零比特填充法:这种方法规定数据帧的定界符为固定的 01111110,即被 0 包围的连续 6 个 1 。对于有效数据部分,扫描一遍,只要遇到连续 5 个 1,便在其后面添加 1 个 0。恢复时,只要遇到连续 5 个 1,便将其后面的 0 删除。

违规编码法:在曼切斯特编码中,每个比特必须含有一次跳变。故有效数据部分不会出现 高-高、低-低 的信号。可以利用这种违规编码作为数据帧定界符。
差错控制
奇偶校验法
在数据的末尾补充一位校验元,得到校验码(信息元+校验元),使得校验码的 ‘1’ 的个数为奇数(奇校验)或偶数(偶校验)。
例如, 1100101 的采用奇校验得到的校验码为 11001011。
这种校验方式十分简单,但是无法识别偶数个比特同时出错的情况,也无法进行纠错。
CRC 校验法
CRC 校验法的思想是:用一个特定的比特序列(生成多项式序列)对原始数据进行模 2 除法,得到的余数(帧检验序列 FCS)作为校验码。
生成多项式是一个预定义的多项式,通常由协议规定。例如,在 IEEE 802.3 标准中,用于以太网帧的 CRC 校验采用的是 CRC-32 算法,其对应的生成多项式如下:
将其转换为比特序列时,将 n 阶的多项式系数转换为序列中对应位的数值即可。例如,x^4+x^1+x^0 对应的比特序列为 10011。
模 2 除法的过程:在长除法的基础上,将每次相减求余改为每次异或求余。用具体例子能更好地理解:

CRC 校验法能确保以非常接近 1 的概率检验出数据的错误,但并不能实现纠错。
海明码
海明距离:
海明距离又称为最小码距。
码距的含义是:两个等长编码,需要经过几次 0到1 或 1到0 的单位变化才能互相转换。例如,101 与 000 的码距是 2。
一个编码集中,编码两两之间的最小码距就是编码集的海明距离。
为了实现 1 位校验,海明距离应该至少为 2,这样每 2 个编码之间至少有 1 个不合法编码。如果数据出现 1 位错误,它将会落在不合法编码区间。显然,为了实现 n 位校验,海明距离应该至少为 n+1。
为了实现 1 位纠错,海明距离应该至少为 3,这样每 2 个编码之间至少有 2 个不合法编码,如果数据出现 1 位错误,与它码距最近的合法数据就是原数据。显然,为了实现 n 位纠错,海明距离应该至少为 2n + 1。
校验码实现 1 位纠错:
- 确定海明码校验码位数
为了能够实现 1 位纠错,校验码的取值数量应该不小于有效数据和校验码的总位数+1(即对应所有位中任意 1 位出错的情况和没有出错的情况)。
设校验码位数为 r,有效数据位数为 n,它们满足如下关系(海明不等式):
- 求海明校验码
在求校验码之前需要对校验码和有效数据编上序号。先依次将第 n 位校验码放在序号为 2^n 的位置上,然后将有效数据按从低到高的顺序填入空位。

接下来,以图中 x_1(即校验码中第 0 位)为例,它将负责校验 序号二进制数形如 **1 的数据,即序号为 1、3、5、7的数据。其中,序号 1 为校验码,序号 3、5、7 为有效数据。对序号 3、5、7 求偶校验码,并将序号 1 设为该值。以上图为例子,x_1 的值应为 1。
其他位类推。
- 纠错
显然,序号形如 **1 的数据出错,当且仅当对应的校验码位无法通过偶校验检测。那么如何定位出错的数据位就很明了了。
首先对每个校验码的位,检查它负责校验的数据是否发生错误,以 x_1 为例,发送的时候,序号 7、5、3、1 对应的数据为 1001。如果收到 1101,不符合偶校验,则认为数据出错。
对于每个校验码的位,如果它负责校验的数据出错,则标记为 1。上例中,标记 x_1=1。如果没有出错,则标记为 0。
最终,校验码从高位到低位排列组成的二进制数,就是出错位序号的二进制数。例如 x_4x_2x_1=101,那么序号为 5 的数据出错。